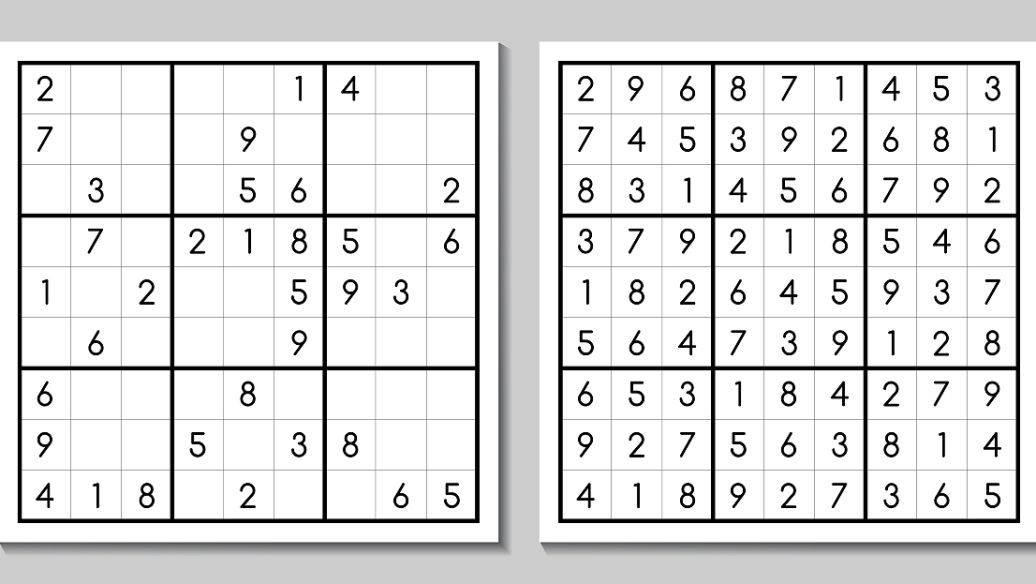
今天介绍一个技巧。这个技巧英文名叫Multi-Sector Locked sets,简写为MSLS。由于它的主体是一个矩阵,纵横相交,像一张网。所以我们习惯称这个方法为矩阵法,或“网”。
这个方法,比单线传递的“链”更高阶。更多地出现在超高难度的题目中。我们也是从老外那里学的,昨天研究了一整天。现在分享出来给大家,希望能够更完善。
参与昨天研讨,以及此贴撰写的几位@whywhite @辉煌背后的衰落 @cobra_zj213 @uFdooW @话不小心 @gyfqbj86 当然或许还有默默关注,或被我遗忘的
其中,尤其感谢@whywhite 最先提供的解释方案,让大家豁然开朗;同时,@辉煌背后的衰落 写出了矩阵的阵列式,从理论的角度给出证明。下文中的描述,有我的个人理解,也有大家的理解。可能会有失真之处,大家可在回帖内补充。
先看一个非常简单的结构图:
这样的结构出现在盘势里,大家用传统的思路去想想,可以删哪些数?

实际删数效果预览:
不信的同学可以找一处验证一下:比如,C3和E3的1如果同时删去,E3=c,E5=2,E8=3,C3=ab,C5=ab,C8=ab。蓝色结构崩溃致死。所以,C3(1)==E3(1)。第三列其余的1可删去。其他删数同理。

这个结构就是一个最最简单的MSLS,2X3的矩阵,即我们俗称的“网”。有同学可能会提出疑问:这个用ALS的思想,稍微想一下也能够解释吧?其实,容易解释是因为这个网很小,而且,其中数字类的候选数,都是“落单”出现的,所以很好理解。下面我们来看一个3X3的网,并且节点候选数更加复杂的网是什么样的。

现在这个例子已经没法单纯用ALS来解释了。我们可以这样看:
矩阵的第一行里,数字类的候选数至少要有一真。(否则,三格都是ab,矛盾)
矩阵的第二行里,数字类的候选数至少要有两真。(否则,有两格是b,矛盾)
矩阵的第三行里,数字类的候选数至少要有两真。(否则,有两格是c,矛盾)
所以,整个矩阵中,数字类的候选数至少有5个为真。
现在来看列:
矩阵的第一列里,字母类候选数至少要有一真。(否则,三格都是12,矛盾)
矩阵的第二列里,字母类候选数至少要有一真。(否则,三格都是13,矛盾)
矩阵的第三列里,字母类候选数至少要有两真。(否则,有两格是4,矛盾)
所以,整个矩阵中,字母类候选数至少有4个为真。
于是,加起来看,整个矩阵中,总共是九个格子,字母类和数字类候选数一共刚好9真。写到这里聪明的同学是不是隐约已经想到什么了,九个小球放到九个格子里,怎么放?
为保险起见,我们细化来看:
其中,通过“行”分析出数字类出现5真,现在看它们在”列“内的分配,只有一种分配方式,就是第一列两真,第二列两真,第三列一真。也就是说不管怎么放,每一列的不同的数字候选数都会出现。
同样地,通过“列”分析出字母类出现4真,现在看它们在”行“内的分配,也只有一种分配方式,就是第一行两真,第二行一真,第三行一真。也就是说不管怎么放,每一行的不同的字母候选数都会出现。
于是,删数效果如图所示:

现在我们能够分析出删数的原理的,但是,找这个结构时,怎么去确定目标格符合结构条件呢?
由于前面已经进行过删数原理分析,所以现在我们来个公式化记忆:
第一行的字母类,出现两种(ab)。
第二行的字母类,出现一种(b)。
第三行的字母类,出现一种(c)。
第一列的数字类,出现两种(12)。
第二列的数字类,出现两种(13)。
第三列的数字类,出现一种(4)。
以上合计九种。只要这个合计数9,等于网的总节点数9,那么,这就是一个标准的网结构。我们就可以用它来删数了。
现在我们来看一个4X4的完整的网的结构。由于是4X4,总共十六个节点,而且我们把数字类和字母类都设定为“互不相同”,所以我们不要让它被九宫限制。现在设想把它出现在一个大于等于十六宫的数独盘里。

我们来验证一下看它是否满足网结构的要求:
每一行,字母类都含两种,合计8种。
每一列,数字类都含两种,合计8种。
总计16种,刚好等于节点数。所以,是满足网结构的。可以进行网式大片删数。
以上是我个人的理解,因为很不成熟,所以可能不全面,或者看不懂等等。所以,接下来我们来学习一下@辉煌背后的衰落 将矩阵法公式化地解释。由于本人对程序化的语言不是很懂,所以这段是原文复制 。
。
↓↓↓↓↓↓↓↓↓↓↓↓辉神的解释↓↓↓↓↓↓↓↓↓↓↓↓
首先,构造矩阵丨Ai aj丨(1≤i≤4,1≤j≤4),i表示行,j表示列,Ai表示i行的数构成的数组,aj表示j行的数构成的数组。
说明:之所以构造到4*4,是因为当i≥5,j≥5时所形成的矩阵,一定能找到一个(9-i)*(9-j)矩阵进行互补。
特例:
先来看一个简单的特殊矩阵:A1=AB A2=CD A3=EF A4=GH a1=12 a2=34 a3=56 a4=78
(矩阵中字母跟数字均指代某一数字,非特指)
AB12 AB34 AB56 AB78
CD12 CD34 CD56 CD78
EF12 EF34 EF56 EF78
GH12 GH34 GH56 GH78
由此矩阵指,所有数字均不相同,知某单一数字只在其所在的行或者列出现,
根据数独规则知,某单一数字在其单元内最多出现1次,即1真,16个数字即最多16真。填入到4*4矩阵,而矩阵的大小为4*4=16,即16个数字全为真,否则会有格无数可填,产生矛盾。
效果S:删 Ai数组所在行,矩阵外的所有格子里的数组Ai;删 aj数组所在列,矩阵外的所有格子里的数组aj。
归纳:
矩阵Aiaj中,Aiaj分别代表一个数字,在这些数字中,部分数字重复出现。将这些数字记为Bxi(x表示具体的数值,所以有x=1、2、...、9;i为x出现的次数,所以有1≤i≤4,因为数独就某一数字而言在同一单元内只出现1次)。
所以,在矩阵中,重复出现的数字总共重复出现的次数和为Σi,表示重复出现的数字最多有Σi个为真;只出现一次的数字的个数为(i*j-Σi),表示这些数字最多有(i*j-Σi)个为真,总计最多有Σi+(i*j-Σi)=i*j个为真。而矩阵内格子个数为i*j,标明矩阵内的所有数字均为真。
效果:
效果=效果S
(此矩阵适用于所有的满足数字个数条件的矩阵,无论2*2、2*3、2*4、3*3、3*4、4*4。此法同样适用2*2、2*3等UR结构,因为矩阵外删数效果没错,之所以最后不符合唯一解定义,只因为出现了这个矩阵本身解题过程中就已经出错了)
下面看几个特殊结构的例题:
2*2,即我们所知的连续环,如
12 13
42 43
删数效果自行体验
2*3,

假设A1行其余各不能删掉{12},即A1最多为1真,aj={3、4、5}数组里至少有2真。2真同时作用到A2行,说明至少有2个6为真,矛盾。同理,其他删数也可同样证得。
3*3

3*4同理与2*3,具体例子请读者自行构造!
下面我们来看个真题:
题目来自无趣同学的分享,也是我们学习这个结构的起因:我感觉中间有个结构很奇怪,像SK-LOOP又像之前我说的ALS-NET(其实以前说的那种就是3X3单数节点的MSLS,上图所示),毒群里问了大家无果,由于本人脸皮较厚,于是去玩家论坛请教了老外,带回了这个技巧。。
一开始,大家都不能理解。@cobra_zj213 将老外的语言转化为图示,由@whywhite 同学最先理解,解释给大家听之后,众人豁然开朗,辉神进一步完善这个解释。。于是才有了这篇分享。。
绿色的候选数,相当于之前我们说的“数字类”,蓝色的,相当于“字母类”。紫色的5,可以看做是“游标”。如果你不能理解,可以分两次考虑,分别看5位于第一行和第三行两个位置的情况。
如果你仔细阅读了本文,相信,应该可以独立推断出,所有红色数字都能够删除。怎么样,这个技巧是不是很犀利呢?

这个方法,比单线传递的“链”更高阶。更多地出现在超高难度的题目中。我们也是从老外那里学的,昨天研究了一整天。现在分享出来给大家,希望能够更完善。
参与昨天研讨,以及此贴撰写的几位@whywhite @辉煌背后的衰落 @cobra_zj213 @uFdooW @话不小心 @gyfqbj86 当然或许还有默默关注,或被我遗忘的
其中,尤其感谢@whywhite 最先提供的解释方案,让大家豁然开朗;同时,@辉煌背后的衰落 写出了矩阵的阵列式,从理论的角度给出证明。下文中的描述,有我的个人理解,也有大家的理解。可能会有失真之处,大家可在回帖内补充。
先看一个非常简单的结构图:
这样的结构出现在盘势里,大家用传统的思路去想想,可以删哪些数?

实际删数效果预览:
不信的同学可以找一处验证一下:比如,C3和E3的1如果同时删去,E3=c,E5=2,E8=3,C3=ab,C5=ab,C8=ab。蓝色结构崩溃致死。所以,C3(1)==E3(1)。第三列其余的1可删去。其他删数同理。

这个结构就是一个最最简单的MSLS,2X3的矩阵,即我们俗称的“网”。有同学可能会提出疑问:这个用ALS的思想,稍微想一下也能够解释吧?其实,容易解释是因为这个网很小,而且,其中数字类的候选数,都是“落单”出现的,所以很好理解。下面我们来看一个3X3的网,并且节点候选数更加复杂的网是什么样的。

现在这个例子已经没法单纯用ALS来解释了。我们可以这样看:
矩阵的第一行里,数字类的候选数至少要有一真。(否则,三格都是ab,矛盾)
矩阵的第二行里,数字类的候选数至少要有两真。(否则,有两格是b,矛盾)
矩阵的第三行里,数字类的候选数至少要有两真。(否则,有两格是c,矛盾)
所以,整个矩阵中,数字类的候选数至少有5个为真。
现在来看列:
矩阵的第一列里,字母类候选数至少要有一真。(否则,三格都是12,矛盾)
矩阵的第二列里,字母类候选数至少要有一真。(否则,三格都是13,矛盾)
矩阵的第三列里,字母类候选数至少要有两真。(否则,有两格是4,矛盾)
所以,整个矩阵中,字母类候选数至少有4个为真。
于是,加起来看,整个矩阵中,总共是九个格子,字母类和数字类候选数一共刚好9真。写到这里聪明的同学是不是隐约已经想到什么了,九个小球放到九个格子里,怎么放?
为保险起见,我们细化来看:
其中,通过“行”分析出数字类出现5真,现在看它们在”列“内的分配,只有一种分配方式,就是第一列两真,第二列两真,第三列一真。也就是说不管怎么放,每一列的不同的数字候选数都会出现。
同样地,通过“列”分析出字母类出现4真,现在看它们在”行“内的分配,也只有一种分配方式,就是第一行两真,第二行一真,第三行一真。也就是说不管怎么放,每一行的不同的字母候选数都会出现。
于是,删数效果如图所示:

现在我们能够分析出删数的原理的,但是,找这个结构时,怎么去确定目标格符合结构条件呢?
由于前面已经进行过删数原理分析,所以现在我们来个公式化记忆:
第一行的字母类,出现两种(ab)。
第二行的字母类,出现一种(b)。
第三行的字母类,出现一种(c)。
第一列的数字类,出现两种(12)。
第二列的数字类,出现两种(13)。
第三列的数字类,出现一种(4)。
以上合计九种。只要这个合计数9,等于网的总节点数9,那么,这就是一个标准的网结构。我们就可以用它来删数了。
现在我们来看一个4X4的完整的网的结构。由于是4X4,总共十六个节点,而且我们把数字类和字母类都设定为“互不相同”,所以我们不要让它被九宫限制。现在设想把它出现在一个大于等于十六宫的数独盘里。

我们来验证一下看它是否满足网结构的要求:
每一行,字母类都含两种,合计8种。
每一列,数字类都含两种,合计8种。
总计16种,刚好等于节点数。所以,是满足网结构的。可以进行网式大片删数。
以上是我个人的理解,因为很不成熟,所以可能不全面,或者看不懂等等。所以,接下来我们来学习一下@辉煌背后的衰落 将矩阵法公式化地解释。由于本人对程序化的语言不是很懂,所以这段是原文复制
↓↓↓↓↓↓↓↓↓↓↓↓辉神的解释↓↓↓↓↓↓↓↓↓↓↓↓
首先,构造矩阵丨Ai aj丨(1≤i≤4,1≤j≤4),i表示行,j表示列,Ai表示i行的数构成的数组,aj表示j行的数构成的数组。
说明:之所以构造到4*4,是因为当i≥5,j≥5时所形成的矩阵,一定能找到一个(9-i)*(9-j)矩阵进行互补。
特例:
先来看一个简单的特殊矩阵:A1=AB A2=CD A3=EF A4=GH a1=12 a2=34 a3=56 a4=78
(矩阵中字母跟数字均指代某一数字,非特指)
AB12 AB34 AB56 AB78
CD12 CD34 CD56 CD78
EF12 EF34 EF56 EF78
GH12 GH34 GH56 GH78
由此矩阵指,所有数字均不相同,知某单一数字只在其所在的行或者列出现,
根据数独规则知,某单一数字在其单元内最多出现1次,即1真,16个数字即最多16真。填入到4*4矩阵,而矩阵的大小为4*4=16,即16个数字全为真,否则会有格无数可填,产生矛盾。
效果S:删 Ai数组所在行,矩阵外的所有格子里的数组Ai;删 aj数组所在列,矩阵外的所有格子里的数组aj。
归纳:
矩阵Aiaj中,Aiaj分别代表一个数字,在这些数字中,部分数字重复出现。将这些数字记为Bxi(x表示具体的数值,所以有x=1、2、...、9;i为x出现的次数,所以有1≤i≤4,因为数独就某一数字而言在同一单元内只出现1次)。
所以,在矩阵中,重复出现的数字总共重复出现的次数和为Σi,表示重复出现的数字最多有Σi个为真;只出现一次的数字的个数为(i*j-Σi),表示这些数字最多有(i*j-Σi)个为真,总计最多有Σi+(i*j-Σi)=i*j个为真。而矩阵内格子个数为i*j,标明矩阵内的所有数字均为真。
效果:
效果=效果S
(此矩阵适用于所有的满足数字个数条件的矩阵,无论2*2、2*3、2*4、3*3、3*4、4*4。此法同样适用2*2、2*3等UR结构,因为矩阵外删数效果没错,之所以最后不符合唯一解定义,只因为出现了这个矩阵本身解题过程中就已经出错了)
下面看几个特殊结构的例题:
2*2,即我们所知的连续环,如
12 13
42 43
删数效果自行体验
2*3,

假设A1行其余各不能删掉{12},即A1最多为1真,aj={3、4、5}数组里至少有2真。2真同时作用到A2行,说明至少有2个6为真,矛盾。同理,其他删数也可同样证得。
3*3

3*4同理与2*3,具体例子请读者自行构造!
下面我们来看个真题:
题目来自无趣同学的分享,也是我们学习这个结构的起因:我感觉中间有个结构很奇怪,像SK-LOOP又像之前我说的ALS-NET(其实以前说的那种就是3X3单数节点的MSLS,上图所示),毒群里问了大家无果,由于本人脸皮较厚,于是去玩家论坛请教了老外,带回了这个技巧。。
一开始,大家都不能理解。@cobra_zj213 将老外的语言转化为图示,由@whywhite 同学最先理解,解释给大家听之后,众人豁然开朗,辉神进一步完善这个解释。。于是才有了这篇分享。。
绿色的候选数,相当于之前我们说的“数字类”,蓝色的,相当于“字母类”。紫色的5,可以看做是“游标”。如果你不能理解,可以分两次考虑,分别看5位于第一行和第三行两个位置的情况。
如果你仔细阅读了本文,相信,应该可以独立推断出,所有红色数字都能够删除。怎么样,这个技巧是不是很犀利呢?